您是否想过我们如何使用机器学习根据过去的数据预测未来的结果？机器学习中使用的最基本的技术之一是线性回归。在本文中，我们将探讨线性回归的基础知识以及如何将其应用于解决现实世界的问题。

假设您是索道系统的所有者，该系统将游客运送到山上观光。你想根据天气情况和索道票价来预测每天的游客数量。

您收集有关过去一年中每一天的游客人数、每日温度、降水量和票价的数据。然后，您可以使用线性回归构建模型，根据天气状况和票价预测游客数量。

首先，您要确定自变量，在本例中为每日气温、降水量和票价。因变量是访问者的数量。

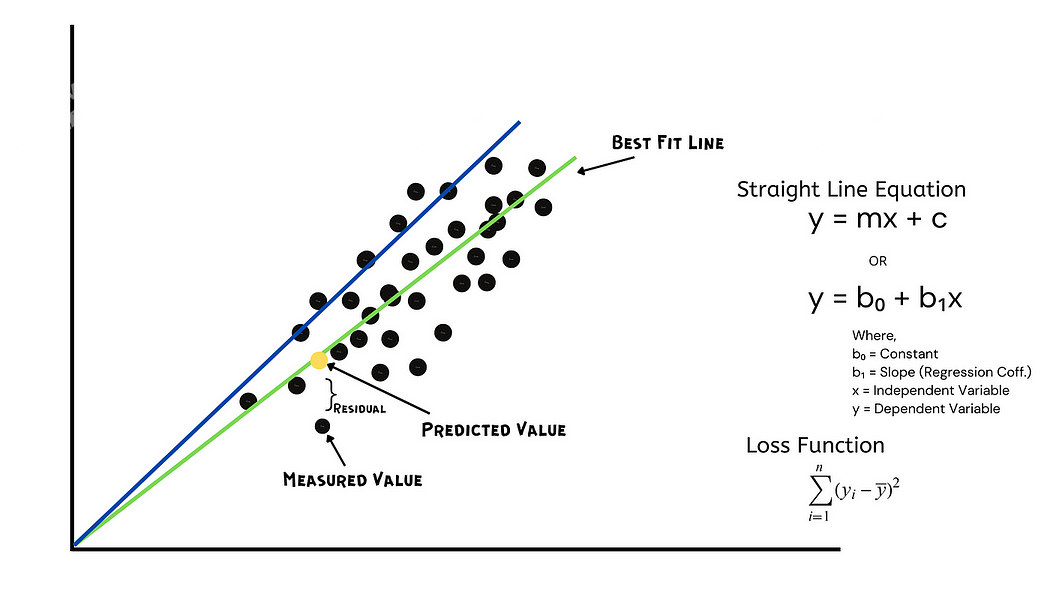
线性回归是一种常用的统计方法，是一种预测分析。它是一种监督算法，回归的中心思想是研究变量之间的数学关系。线性回归有助于确定因变量（结果）与自变量（输入）的关联程度以及该关系的性质，无论是正还是负。我们借助最佳拟合线（也称为回归线）找到它们之间的关系。

一条线的方程是，y = mx + c

在这个等式中：

y 代表因变量，在这种情况下是索道的游客数量。

x 表示自变量，在本例中可以是温度、降水量或票价。

m代表直线的斜率，它决定了自变量和因变量之间的关系。换句话说，它表示自变量每增加一个单位，因变量的变化量。

c代表y轴截距，也就是直线与y轴相交的点。

在索道示例的上下文中，方程式可以写为：

访客数 = m1 x 温度 + m2 x 降水量 + m3 x 票价 + c

让我们了解一下 Python 中线性回归的暴力破解代码。

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression


# Load data into a Pandas DataFrame
df = pd.read_csv('your dataset location')
# Split data into independent and dependent variables
X = 'Your independent features'
y = 'Your dependent features'

# Create a linear regression model and fit it to the data
model = LinearRegression()
model.fit(X, y)


# Use the model to make predictions
new_data ='Your transformed data'
predicted_visitors = model.predict(new_data)

# Create a scatter plot of actual visitors versus predicted visitors
plt.scatter(y, model.predict(X))
plt.scatter(predicted_visitors, predicted_visitors, color='red')
plt.xlabel('your actual labels ')
plt.ylabel('your Predicted labels')
plt.show()

线性回归模型的主要假设：

线性：自变量和因变量应呈线性关系，这样自变量的变化将导致因变量按比例变化。

无多重共线性：实际值与预测值之间的差异对于自变量的所有水平应呈正态分布（数据应在多个维度上服从正态分布）。

正态性：回归模型的误差应该在零附近呈正态分布。

同方差性：因变量的可变性在自变量的所有值之间是一致的。

选型技巧：

逐步回归：逐步回归有两种类型：向前选择和向后淘汰。

前向选择：此方法从一个不包含变量的模型开始，并根据变量的重要性一次添加一个变量。在每一步中，将对模型拟合提供最大改进的变量添加到模型中，直到没有更多变量可以改进拟合为止。

逆向淘汰：此方法从一个包含所有变量的模型开始，并根据变量的重要性一次删除一个变量。在每个步骤中，从模型中删除对模型拟合提供最小改进的变量，直到没有更多变量可以删除而不会显着降低拟合

信息准则：最常用的信息准则是 Akaike 信息准则 (AIC) 和贝叶斯信息准则 (BIC)，它们提供了一种根据拟合优度和使用的参数数量来比较不同模型的方法在模型中。

正则化：正则化方法，例如岭回归和套索回归，在回归方程中添加一个惩罚项，以将不太重要的变量的系数缩小到零。这有助于降低多重共线性的影响，提高模型的泛化能力。

交叉验证：交叉验证涉及将数据拆分为训练集和测试集，然后评估模型在测试集上的性能。这有助于防止过度拟合并确保模型可推广到新数据。

解释机器学习模型结果的技术

R 平方：R 平方是一种统计量度，表示因变量中由自变量解释的方差的比例。它的范围从 0 到 1，值越高表示模型对数据的拟合越好。

在索道示例中，线性回归模型的 R 平方值告诉我们游客数量的变化有多少可以用自变量（温度、降水量和票价）来解释。例如，如果 R 平方值为 0.8，则表示访客数量的 80% 的变化可以由自变量解释，而其余 20% 是由模型中未包含的其他因素引起的.

平均绝对误差 (MAE)：平均绝对误差 (MAE) 是衡量模型实际值和预测值之间平均绝对差值的指标。在索道示例的上下文中，MAE 可用于评估线性回归模型根据温度、降水量和票价预测索道游客数量的效果。

均方根误差 (RMSE)：均方根误差 (RMSE) 是用于评估回归模型性能的另一种流行指标。它测量预测值和实际值之间的平方差的平均值的平方根。

均方误差 (MSE)：此技术计算实际值和预测值之间的平方差的平均值。它给出了误差项中有多少方差的想法。

现实生活中的例子

交通流量分析：线性回归可用于模拟交通流量与各种因素（例如一天中的时间、天气状况等）之间的关系。

运动分析：线性回归可以成为运动分析中的有用工具，可以深入了解球员的表现并围绕球队管理和球员选择做出明智的决策。

资产定价：线性回归可用于分析各种金融变量与资产价格之间的关系。这可以帮助投资者根据他们的预期未来回报，就购买或出售哪些资产做出明智的决定

价格优化：线性回归可用于分析产品定价与销量之间的关系。这可以帮助公司优化他们的定价策略以最大化销售和利润。